Block-stacking problem
In statics, the block-stacking problem (also the book-stacking problem, or a number of other similar terms) is the following puzzle:
Place
rigid rectangular blocks in a stable stack on a table edge in such a way as to maximize the overhang.
The single-wide problem involves having only one block at any given level. In the ideal case of perfectly rectangular blocks, the solution to the single-wide problem is that the maximum overhang is given by 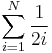 times the width of a block. This sum is one half of the harmonic series. The maximal overhang tends to infinity as
times the width of a block. This sum is one half of the harmonic series. The maximal overhang tends to infinity as  increases, meaning that it is possible to achieve any arbitrarily large overhang, with sufficient blocks.
increases, meaning that it is possible to achieve any arbitrarily large overhang, with sufficient blocks.
Multiwide stacks using counterbalancing can give larger overhangs than a single width stack. Even for three blocks, stacking two counterbalanced blocks on top of another block can give overhang close to 1, while the overhang in the simple ideal case is at most 11/12. As Paterson et al. (2007) showed, asymptotically, the maximum overhang that can be achieved by multiwide stacks is proportional to the cube root of the number of blocks, in contrast to the single-wide case in which the overhang is proportional to the logarithm of the number of blocks.
Paterson et al. provide a long list of references on this problem going back to mechanics texts from the middle of the 19th century. Hall (2005) discusses this problem, shows that it is robust to nonidealizations such as rounded block corners and finite precision of block placing, and introduces several variants including nonzero friction forces between adjacent blocks.
References
- Hall, J. F. (2005). "Fun with stacking blocks". American Journal of Physics 73 (12): 1107–1116. doi:10.1119/1.2074007.
- Paterson, Mike; Peres, Yuval; Thorup, Mikkel; Winkler, Peter; Zwick, Uri (2007). "Maximum overhang". arXiv:0707.0093 [math.HO]..